In this quick clip from Avengers: Age of Ultron (you can see it here), Thor tosses his hammer (Mjölnir) up into the air and catches it. Why does he do this? Because he’s Thor. That’s just what Thor does.
It might seem like a simple trick, but is there any hidden physics here? YES! After the hammer leaves Thor’s hand, there is only one force acting on it—the gravitational force. Even though the hammer is rotating while in the air, the center of mass should move just like a point particle.
So, here is the question: can I look at the motion of Mjölnir and use that to find its center of mass? If so, what does the location of the center of mass say about the hammer?
If I knew the location of the center of mass for the hammer, I could just mark that location in each frame and this would be a very short blog post. So, instead I will have to use the motion of the two ends of the hammer to find the center of mass.
Step 1 is to load the video into Tracker Video Analysis. From here, I am going to estimate that the width of the hammer is 15 cm. Once I mark the top and bottom of the hammer, I get the following plot for the vertical motion.
Of course, there a couple of problems with this video clip. First, there are only a few frames in which both the top and bottom of the hammer can be seen at the same time. Second, the hammer is angled towards the camera instead of the optimal viewing angle that showing the hammer from the side. However, I will proceed anyway (as usual).
What I want to look for is a location in between the top and the bottom of the hammer that has a vertical acceleration of -9.8 m/s 2. This means that I just need to plot different points along the hammer and find the vertical acceleration. To do this, I will break the hammer into small sections. By calculating the distance from the top of the hammer to the bottom (this appears to change as the hammer rotates), I can then multiple by a factor (say 0.1) to get a vertical position 1/10 th the way from the bottom to the top. When I plot that position, I can then find the acceleration.
Here is the vertical acceleration for the different part. The horizontal axis is the fraction of the way from the bottom of the hammer to the top.
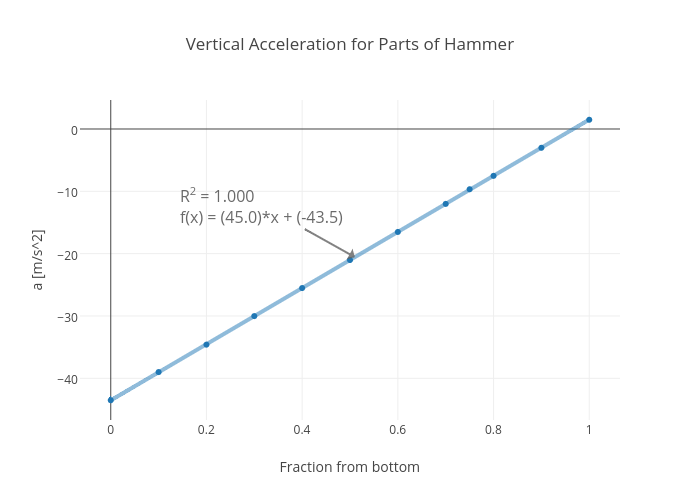I could use the linear function that fits the data to find the location where the acceleration is around -9.8 m/s 2 — but just guessing, it looks like 0.75 of the way from the bottom to the top is pretty close. I’ll just use that value. Now I can do the same thing while looking at the horizontal motion of the hammer. The big difference is that the acceleration of the center of mass should be zero. Instead of fitting a quadratic equation to the data, I will fit a linear function and the slope of this function will be the horizontal velocity.
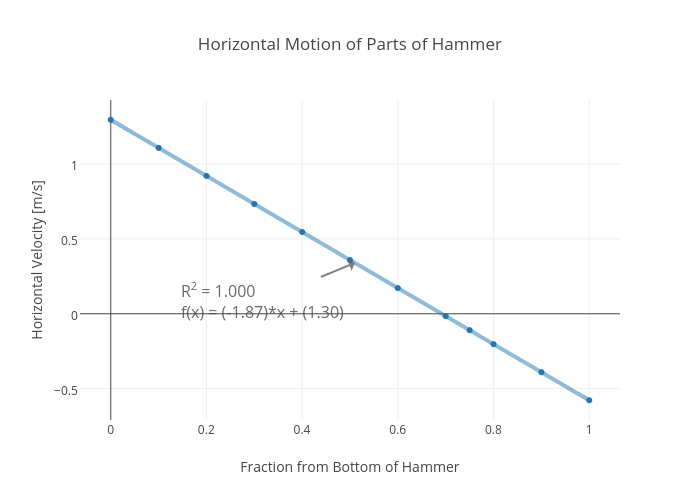This data is a bit more difficult to use. Since the different parts of the hammer move towards or away from the camera, it’s tough to say what the velocity should be. My best guess is that since Thor tosses and then catches the hammer, it should have close to a zero horizontal velocity. This seems to suggest that my center of mass location of around 0.75 from the bottom might be ok.
Where would this be on the hammer? Here is the hammer from the same clip. If I measure 0.75 from the bottom, the center of mass would be the white circle.
Mjölnir is obviously not a normal hammer (here is an excellent post looking at the density of Mjölnir). However, let’s just treat the hammer as two separate objects there is the head (the big rectangular part) and then there is the handle. If I assume both the head and the handle are uniform densities then I can turn this into a classic center of mass problem since both parts will have their own center of masses in their centers.
Now that I have essentially just two point masses, I can write the total center of mass as:
If I use estimated hammer dimensions from the movie, I will say the length of the head is 26.3 cm (with a height of 16 cm) with a handle length of 42.8 cm. So now I have the location of the center of mass, the center of the handle and the center of the head. With this I can solve for the ratio of masses for the head to handle.
The best way to find the ratio of handle to head mass is to consider torque. If the hammer was balanced at the center of mass, then the torque from the handle must be opposite the torque from the head. I will call the distance from the center of mass to the handle a distance s 1 and the distance to the head s 2. This gives the following ratio (here is my best explanation of center of mass and torque):
Putting in my values for the distances, I get a handle to head mass ratio of 0.295. Big deal, right? Ok, let’s use this to estimate the ratio of densities for the handle and the head. I will assume the handle is a cylinder with a diameter of 5.4 cm which gives it a volume of 980 cm 3. The head has a volume of 6312 cm 3. From this, and the definition of density, I can find the ratio of densities.
Using my values, I get a density ratio of 1.9. The density of the material in the handle is almost twice that of the head. Is that odd? That’s odd. Well, it’s not odd if the hammer isn’t the REAL Mjölnir. Maybe it’s just a prop with an aluminum tube handle and a wooden head. I wonder if Thor knows his hammer is fake.
Oh, just for fun. If the handle and the head were made of the same material, I could find the ratio of masses based on their volumes. From this m 1 /m 2 would be 0.155. This would put the center mass 46.8 cm from the bottom of the handle (or 4 cm higher than in the clip).
Now for one homework assignment. Here is a video where I toss two different (but real) hammers. One is a rubber mallet with a low mass head and the other has a steel head.
